Дифференцированный платеж, аннуитетные платежи, схема и расчет дифференцированного платежа
Дифференцированный платеж – универсальная и самая выгодная система погашения любого кредита. Найти отечественный банк, который работает по такому принципу не просто, но возможно. Время, потраченное на поиски, с лихвой компенсируется удобством и выгодой в процессе погашения займа.
Содержание
Скрыть- Дифференцированный платеж
- Аннуитетные и дифференцированные платежи
- Схема дифференцированного платежа
- Расчет дифференцированного платежа
Дифференцированный платеж
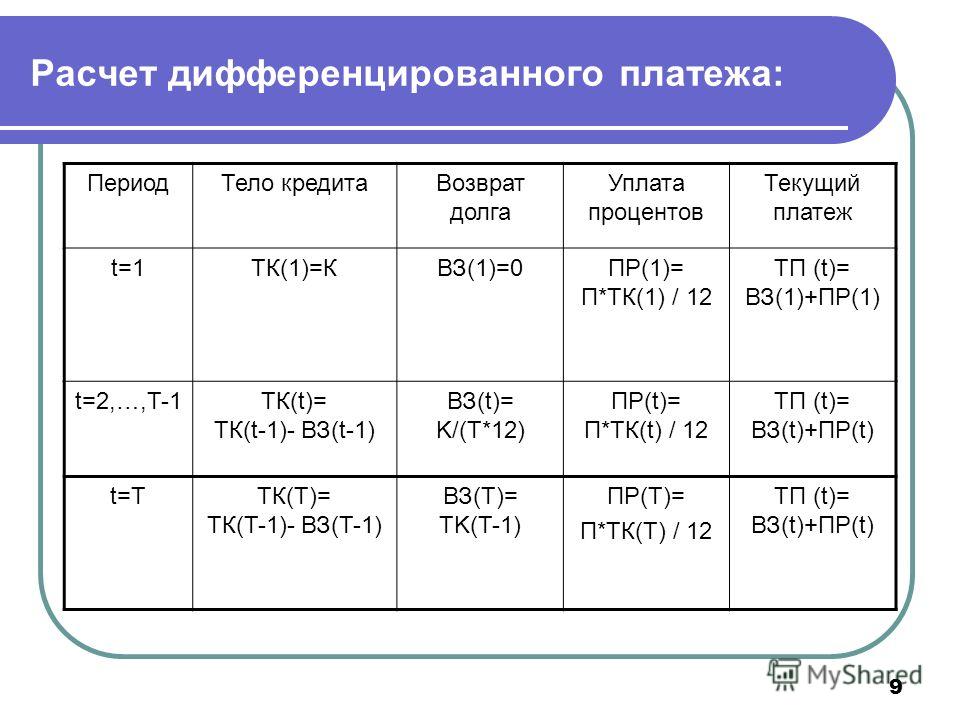
Дифференцированные платежи как схема погашения кредита удобна тем, что заемщик рассчитывается с кредитором путем выплат равных частей тела кредита на фоне планомерного уменьшения ежемесячной суммы платежа. Происходит это за счет уменьшения тела кредита и сокращения объема процентной части.
Единственным недостатком дифференцированной системы считается необходимость подготовиться к серьезной финансовой нагрузке в начале срока кредитования.
Аннуитетные и дифференцированные платежи
Аннуитетные схемы погашения кредита кажутся большинству заемщиков более удобными, поскольку сумма ежемесячного взноса остается фиксированной на протяжении всего периода погашения. Но этот принцип разработан банкирами специально, чтобы сократить путь к потенциально большему размеру дохода. Если сравнивать сумму переплаты по дифференцированному кредиту и аннуитету при одинаковых условиях выдачи займа, цифры гарантированно скажут в пользу первого варианта.
Несмотря на кажущуюся простоту, большая часть первых аннуитетных платежей процентная. Фактически это означает, что в первые несколько лет заемщик оплачивает банку стоимость кредита, и только после этого начинает уменьшаться реальная сумма задолженности.
Схема дифференцированного платежа
Если вы готовы работать на перспективу и значительно урезать текущие расходы на начальном этапе кредитования – выбирайте займ с дифференцированной системой погашения.
Первые месяцы, а в ряде случаев и годы пролетают достаточно быстро, зато большую часть периода погашения заимствованных средств ежемесячный платеж станет более щадящим для кошелька и менее обременительным для семейного бюджета.
Среди финансовых продуктов российской банковской системы дифференцированные алгоритмы погашения предлагаются преимущественно в рамках ипотечного кредитования, хотя отдельные учреждения занимаются потребительским кредитованием по такому же принципу. При оформлении долгосрочного кредита финансовые аналитики настоятельно рекомендуют внимательнее присмотреться к возможности оформления займа на условиях погашения дифференцированными платежами.
Расчет дифференцированного платежа
Рассчитать сумму дифференцированного платежа несложно. Достаточно сумму кредита разделить на количество месяцев периода кредитования, после чего остается составить удобный для заемщика график платежей. Процентная часть платежа уменьшается с каждым месяцем, поскольку начисляется на постоянно уменьшающийся объем тела кредита.
Универсальная формула расчета месячного дифференцированного платежа выглядит следующим образом: х= s/n+s*P*d/G/100
Расшифровка значений формулы:
х – ежемесячный дифференцированный платеж;
s– размер тела кредита на дату расчета процентной части по очередному платежу;
P – размер годовой процентной ставки;
d – количество дней в расчетном периоде;
G – количество дней в текущем году;
N – число оставшихся процентных периодов (месяцев).
Совет от Сравни.ру: У дифференцированных и аннуитетных кредитов есть свои плюсы и минусы. Но если задействовать чистую арифметику и определить итоговый финансовый результат, оформление займа с дифференцированной системой погашения более выгодно для заемщика и менее привлекательно для коммерческого банка.
Дифференцированный платеж — расчет, формула
Дифференцированный платеж — вариант ежемесячного платежа по кредиту, когда размер ежемесячного платежа по погашению кредита постепенно уменьшается к концу периода кредитования.
Ежемесячный платёж, при дифференцированной схеме погашения кредита, состоит из двух составляющих. Первая часть называется основным платежом, размер которого не изменяется на всём сроке кредитования. Основной платёж идет на погашения основного долга по кредиту. Вторая часть — убывающая, которая уменьшается к концу срока кредитования. Данная часть платежа идет на погашение процентов по кредиту.
При дифференцированной схеме погашения кредита, ежемесячный платеж рассчитывается как сумма основного платежа и проценты, начисляемые на оставшийся размер долга. Естественно, что оставшийся размер долга уменьшается к концу срока кредитования, отсюда и получается уменьшение размера ежемесячной выплаты.
Для расчёта размера основного платежа и начисленных процентов можно воспользоваться кредитным калькулятором, на сайте www.platesh.ru, либо воспользоваться обычным калькулятором.
Расчёт дифференцированного платежа
Размер основного платежа вычисляется следующим образом: необходимо сумму кредита разделить на количество месяцев, за который планируется погашение кредита, полученное число и будет являться основным платежом.
| b = S / N , где b – основной платёж, S – размер кредита, N – количество месяцев. |
Для расчета начисленных процентов нужно остаток кредита на указанный период умножить на годовую процентную ставку и всё это поделить на 12 (количество месяцев в году).
| p = Sn * P / 12, где p – начисленные проценты, Sn — остаток задолженности на период, P – годовая процентная ставка по кредитy. |
Чтобы рассчитать остаток задолженности на период, т.е. найти величину из приведённой выше формулы, необходимо размер основного платежа умножить на количество прошедших периодов и всё это вычесть из общей суммы платежа.
| Sn = S — (b * n) , где n – количество прошедших периодов. |
Пример расчёта графика выплат по дифференцированному кредиту
Для примера рассчитаем график платежей по кредиту в размере 100000 р.
Определим размер основного платежа:
Определим размер выплаты за каждый месяц периода кредитовния:
| Первый месяц: 16666,67 + (100000 – (16666,67 * 0))*0,1/12 = 17500 Второй месяц: 16666,67 + (100000 – (16666,67 * 1))*0,1/12 = 17361,11 Третий месяц: 16666,67 + (100000 – (16666,67 * 2))*0,1/12 = 17222,22 Четвёртый месяц: 16666,67 + (100000 – (16666,67 * 3))*0,1/12 = 17083,33 Пятый месяц: 16666,67 + (100000 – (16666,67 * 4))*0,1/12 = 16944,44 Шестой месяц: 16666,67 + (100000 – (16666,67 * 5))*0,1/12 = 16805,56 |
Если интересно узнать размер переплаты по кредиту, то необходимо сложить ежемесячные выплаты и вычесть из суммы первоначальный размер кредита. Для нашего примера размер переплаты таков:
| 17500 + 17361,11 + 17222,22 + 17083,33 + 16944,44 + 16805,56 – 100000 = 2916,67 |
Результат подсчётов по нашему примеру на сайте www.
platesh.ru будет выглядеть так:
Форма ввода данных для расчёта дифференцированного платежа
Пример графика дифференцированных платежей
Что подтверждает правильность наших расчётов.
методика и формулы расчета процентов и графика платежей
Особенность расчета процентов и графика платежей при дифференцированном способе заключается в равномерном погашении тела кредита на протяжении всего срока кредитования. Другими словами, первоначальная сумма кредита делится на срок кредитования, выраженный в месяцах (количество месяцев) в результате чего определяется доля ежемесячного платежа, закрывающая основную задолженность. Для беспроцентных кредитов все расчеты на этом бы и заканчивались, однако в жизни за полученные в долг денежные средства приходится расплачиваться начисляемыми процентами. С поправкой на этот печальный факт ежемесячный платеж складывается из двух составляющих – погашения основной задолженности и процентов, начисленных на остаток этой задолженности.
Формула для расчета суммы погашения тела кредита за один месяц выглядит следующим образом:
СТК – сумма погашения тела кредита за один месяц;
ТК – сумма тела кредита;
k – количество месяцев.
Начисленные за месяц проценты рассчитываются по следующей формуле:
СП – сумма процентов, начисленных за месяц;
СЗ – сумма задолженности по кредиту;
Таким образом, размер ежемесячного дифференцированного платежа определяется по формуле:
Некоторые банки исходят не из количества месяцев в году, а из количества дней. Тогда формула выглядит следующим образом:
d – число дней в текущем месяце.
ДП – величина платежа за расчетный месяц.
С практическим применением данной методики можно ознакомиться на следующих примерах:
Аннуитетный и дифференцированный платеж — что это? В чем разница и что лучше на 2021 год?
Кредиты играют важную роль в жизни населения со средним достатком. Тем, кто не может позволить себе единовременную оплату из собственных средств при покупке недвижимости или другого дорогостоящего имущества, кредиты очень сподручны. Вот только будущий процесс выплат по таким заёмным средствам для многих изначально остаётся загадкой, и что такое аннуитетный и дифференцированный платёж — знают немногие.
Чтобы сориентироваться в ежемесячных взносах по кредиту и не остаться перед фактом неподъёмных сумм, рассмотрим, какие бывают виды платежей.
Виды платежей по кредитам
Уже после подписания кредитного договора заёмщик вдруг обнаруживает, что первые взносы по кредиту существенно превышают тот возможный лимит, который он может безболезненно выделить на погашение кредитных сумм из своих доходов.
В дальнейшем, чтобы сводить концы с концами и не допустить просрочек по оплате, кредитополучателям приходится «затянуть поясок потуже» или занимать у знакомых и друзей недостающие суммы. В чём же разница между аннуитетным и дифференцированным платежами и какой платёж выгоднее?
Дифференцированные платежи
Ещё в недавние времена в российской (советской) практике кредитования применялся только один вид платежей — дифференцированный. Дифференцированный платёж заключается в том, что на первые месяцы выплат приходятся максимальные суммы, в которые входит часть основного долга и проценты по кредиту.
При дифференцированных платежах сумма основного долга, так называемое тело долга, делится равными частями на весь срок платежа, а вот проценты ежемесячно начисляются на остаток долга. Соответственно, в первый месяц суммы платежей наиболее велики, потому что проценты по кредиту существенны.
А к концу срока выплаты будут минимальны. Дифференцированные платежи удобны для тех, у кого доход не носит характер неизменной величины, и через некоторое время может появиться возможность досрочно погасить долг.
В этом случае переплата по кредиту будет меньше, чем при аннуитетном расчёте.
Далеко не каждый кредитополучатель может позволить себе выплачивать в первые месяцы суммы, складывающиеся при дифференцированном расчёте платежей. Ему придётся отказаться от подобного кредита, либо взять сумму меньшую, чем необходимо, чтобы беспроблемно расплачиваться по долговым обязательствам. Такому заёмщику больше подойдёт аннуитетный вид платежа.
Аннуитетные платежи
Отличие аннуитетного платежа от дифференцированного в том, что сумма ежемесячного взноса всегда неизменна, но вот структура этой суммы меняется из месяца в месяц. Основную часть в первые месяцы составляют проценты по кредиту, а сумма тела долга — минимальна. Таким образом банк страхует риски недополучения прибыли в случае досрочного погашения кредита заёмщиком. Подобный график погашения платежей с ежемесячной суммой — константа очень выгоден людям, имеющим фиксированный доход:
- нет необходимости каждый месяц сверяться с графиком платежей, чтобы заранее зарезервировать нужную сумму для оплаты кредита;
- равные доли платежа позволяют исключить возможность остаться без средств к существованию после уплаты ежемесячного взноса.
Формулы расчёта кредитных платежей
Для того, что бы определить для себя, что лучше: аннуитетный или дифференцированный платёж, можно заранее просчитать по формулам ежемесячные суммы:
- общего платёжа;
- начисляемых процентов;
- суммы основного долга;
- остатка кредита на начало и конец месяца.
Формула расчёта дифференцированного платежа:
- НП — начисленные проценты в периоде;
- ОК — остаток кредита в месяце;
- ПС — процентная ставка по кредиту.
Такая формула часто применяется банками и кредитными учреждениями для расчёта дифференцированных платежей. Общую сумму переплаты по этому виду кредита можно увидеть в таблице:
Формула расчёта аннуитетного платежа:
- АП — общий аннуитетный платёж в периоде;
- СК — первоначальная сумма кредита;
- ПС — процентная ставка по кредиту;
- КП — количество месяцев (периодов).
Данная формула считается основной для расчёта аннуитетных платежей и применяется основным количеством банков и кредитных организаций, используясь в большинстве кредитных калькуляторов. Полученные результаты по ежемесячному погашению кредита и сумме переплаты за пользование займом, можно увидеть в таблице:
Из приведённых расчётов видно, что окончательная сумма переплаты по дифференцированному виду платежа несколько ниже, чем при аннуитетном расчёте. Если сумма кредита существенна, то разница будет более чем очевидна. Таким образом, прежде чем заключить договор по кредитованию, необходимо взвесить все плюсы и минусы обоих видов платежей: дифференцированного и аннуитетного.
Видео: Что выбрать — аннуитетный или дифференцированный платеж?
Итого
Предварительный расчёт поможет определить, что выгоднее заёмщику: переплатить в итоге определённую сумму или удовлетвориться фиксированным ежемесячным платежом.
В наступившем 2021 году правильный расчёт и определение потенциала своего финансового состояния будет более чем актуально.
Читайте также:
Дифференцированные платежи по кредиту в EXCEL. Примеры и описание
Составим в MS EXCEL график погашения кредита дифференцированными платежами.
При расчете графика погашения кредита дифференцированными платежами сумма основного долга делится на равные части пропорционально сроку кредитования. Регулярно, в течение всего срока погашения кредита, заемщик выплачивает банку эти части основного долга плюс начисленные на его остаток проценты. Если кредитным договором период погашения установлен равным месяцу, то из месяца в месяц сумма основного долга пропорционально уменьшается. Поэтому при дифференцированных платежах основные расходы заемщик несет в начале кредитования, размеры ежемесячных платежей в этот период самые большие.
Но постепенно, с уменьшением остатка ссудной задолженности, уменьшается и сумма начисленных процентов по кредиту. Выплаты по кредиту значительно сокращаются и становятся не такими обременительными для заемщика.
Примечание . При расчете кредита дифференцированными платежами сумма переплаты по процентам будет ниже, чем при аннуитетных платежах . Не удивительно, что сегодня практически все российские банки применяют в расчетах аннуитетную схему погашения кредита. Сравнение двух графиков погашения кредита приведено в статье Сравнение графиков погашения кредита дифференцированными аннуитетными платежами в MS EXCEL .
График погашения кредита дифференцированными платежами
Задача . Сумма кредита =150т.р. Срок кредита =2 года, Ставка по кредиту = 12%. Погашение кредита ежемесячное, в конце каждого периода (месяца).
Решение. Сначала вычислим часть (долю) основной суммы кредита, которую заемщик выплачивает за период: =150т.
р./2/12, т.е. 6250р. (сумму кредита мы разделили на общее количество периодов выплат =2года*12 (мес. в году)). Каждый период заемщик выплачивает банку эту часть основного долга плюс начисленные на его остаток проценты. Расчет начисленных процентов на остаток долга приведен в таблице ниже – это и есть график платежей.
Для расчета начисленных процентов может быть использована функция ПРОЦПЛАТ(ставка;период;кпер;пс), где Ставка — процентная ставка за период ; Период – номер периода, для которого требуется найти величину начисленных процентов; Кпер — общее число периодов начислений; ПС – приведенная стоимость на текущий момент (для кредита ПС — это сумма кредита, для вклада ПС – начальная сумма вклада).
Примечание . Не смотря на то, что названия аргументов совпадают с названиями аргументов
функций аннуитета
–
ПРОЦПЛАТ()
не входит в группу этих функций (не может быть использована для расчета параметров аннуитета).
Примечание . Английский вариант функции — ISPMT(rate, per, nper, pv)
Функция ПРОЦПЛАТ() предполагает начисление процентов в начале каждого периода (хотя в справке MS EXCEL это не сказано). Но, функцию можно использовать для расчета процентов, начисляемых и в конце периода для это нужно записать ее в виде ПРОЦПЛАТ(ставка;период-1;кпер;пс), т.е. «сдвинуть» вычисления на 1 период раньше (см. файл примера ). Функция ПРОЦПЛАТ() начисленные проценты за пользование кредитом указывает с противоположным знаком, чтобы отличить денежные потоки (если выдача кредита – положительный денежный поток («в карман» заемщика), то регулярные выплаты – отрицательный поток «из кармана»).
Расчет суммарных процентов, уплаченных с даты выдачи кредита Выведем формулу для нахождения суммы процентов, начисленных за определенное количество периодов с даты начала действия кредитного договора.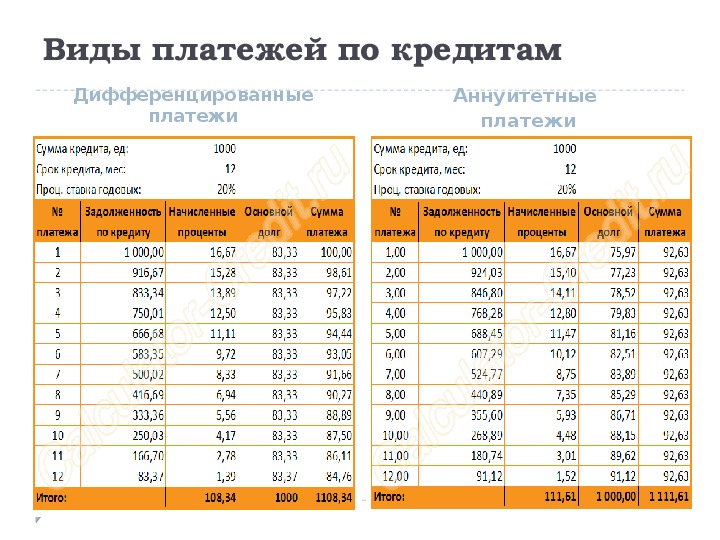
Запишем суммы процентов начисленных в первых периодов (начисление и выплата в конце периода): ПС*ставка (ПС-ПС/кпер)*ставка (ПС-2*ПС/кпер)*ставка (ПС-3*ПС/кпер)*ставка … Просуммируем полученные выражения и, используя формулу суммы арифметической прогрессии, получим результат. =ПС*Ставка* период*(1 — (период-1)/2/кпер) Где, Ставка – это процентная ставка за период (=годовая ставка / число выплат в году), период – период, до которого требуется найти сумму процентов. Например, сумма процентов, выплаченных за первые полгода пользования кредитом (см. условия задачи выше) = 150000*(12%/12)*6*(1-(6-1)/2/(2*12))=8062,50р. За весь срок будет выплачено =ПС*Ставка*(кпер+1)/2=18750р. Через функцию
ПРОЦПЛАТ()
формула будет сложнее: =СУММПРОИЗВ(ПРОЦПЛАТ(ставка;СТРОКА(ДВССЫЛ(«1:»&кпер))-1;кпер;-ПС))
Кредитный калькулятор с досрочным погашением
Данный онлайн калькулятор имеет расширенный набор функций по сравнению со стандартным кредитным калькулятором. Помимо функции расчета досрочного погашения кредита, здесь есть возможность задать изменение процентной ставки, выбрать день выдачи кредита, выбрать день для ежемесячного платежа, выбрать тип ежемесячного платежа — аннуитетный или дифференцированный.
Благодаря этим функциям калькулятор позволяет сделать расчет максимально близким к реальному кредиту, с точностью до дня.
С нашим калькулятором вы сможете рассчитать досрочное погашение кредита за две минуты без визита в банк. Для этого нужно заполнить несколько дополнительных полей в форме калькулятора:
- Дату досрочного внесения средств (если платеж единоразовый) или интервал (если вы собираетесь делать платежи на регулярной основе, например раз в 3 месяца)
- Сумму досрочного платежа
- Выбрать способ перерасчета кредита
Можно задать неограниченное количество частично досрочных погашений.
Особенности частично досрочного погашения кредита
При частично досрочном погашении возможно два типа списаний:
- в день очередного платежа. В этом случае сумма долга просто уменьшается на сумму внеочередного платежа.
- между двумя очередными платежами. Здесь расчет происходит сложнее. Проценты на сумму долга начисляются каждый день, а гасятся раз в месяц. К моменту досрочного платежа накапливается некая сумма процентов, которая будет погашена за счет средств, предназначенных на досрочный платеж. И только оставшаяся сумма пойдет на погашение основного долга. В следующем же месяце процентная часть очередного платежа будет меньше, ведь часть процентов за этот месяц уже уплачена. Не стоит беспокоиться по этому поводу и откладывать досрочное погашение на день очередного платежа. Чем раньше платеж будет зачислен, тем выгоднее.
К моменту досрочного платежа накапливается некая сумма процентов, которая будет погашена за счет средств, предназначенных на досрочный платеж. И только оставшаяся сумма пойдет на погашение основного долга. В следующем же месяце процентная часть очередного платежа будет меньше, ведь часть процентов за этот месяц уже уплачена. Не стоит беспокоиться по этому поводу и откладывать досрочное погашение на день очередного платежа. Чем раньше платеж будет зачислен, тем выгоднее.После внесения внеочередного платежа меняется график последующих погашений кредита. Сумма основного долга уменьшается и следом за ней изменяется один из двух параметров: сумма ежемесячного платежа или срок кредита. Выбор всегда за клиентом банка. С учетом вашего выбора банк делает перерасчет кредита и формирует новый график платежей. Имейте это ввиду и получайте новый график платежей в офисе банка или в программе интернет-банк (если такую возможность предоставляет банк). Наш онлайн калькулятор также позволяет выбрать любой вариант и производит расчет с учетом выбора.
После расчета вам будет представлен подробный график платежей с учетом указанных досрочных погашений.
Выгоднее уменьшать срок кредита, так как общая переплата в этом случае снизится более значительно. Поэтому, если сумма ежемесячного платежа вам посильна, рекомендуем уменьшать именно срок.
Экспериментируйте с параметрами для выбора наиболее подходящего для вас способа перерасчета. Кредитный калькулятор позволяет сохранять результаты расчетов, это очень удобно для сравнения полученных вариантов, так как вам не придется повторно вносить исходные данные кредита в форму.
Изменяемая процентная ставка
Нередко бывает, когда процентная ставка меняется в ходе срока кредита. Это может быть вызвано пересмотром кредитной ставки банком по заявлению заемщика или условиями договора. Для таких ситуаций в калькуляторе предусмотрена соответствующая функция. Можно задать неограниченное количество изменений процентной ставки на протяжении срока кредита. Для каждого периода нужно выбрать дату начала действия ставки и её значение.
Эти изменения также будут отображены и помечены особым цветом в графике платежей.
Страница не найдена
А Армавир Амурск Ангарск
Б Бикин Благовещенск Белогорск Биробиджан
В Владивосток Ванино Вяземский Волгоград Волжский Вологда Воронеж
Д Де-Кастри
Е Екатеринбург
И Иркутск
К Казань Краснодар Красноярск Комсомольск-на-Амуре Калининград Киров
М Москва
Н Нефтекамск Новороссийск Находка Николаевск-на-Амуре Нижний Новгород Новосибирск Нижний Тагил
О Октябрьский Омск
П Петрозаводск Переяславка Пермь
Р Ростов-на-Дону Рязань
С Санкт-Петербург Стерлитамак Сегежа Сыктывкар Сочи Ставрополь Советская Гавань Солнечный Соловьевск Самара Саратов
Т Туймазы Тында Томск Тюмень
У Уфа Ухта Уссурийск
Х Хабаровск Хор
Ч Чегдомын Челябинск Чита
Ю Южно-Сахалинск
Как сделать дифференцированный платеж
Возможны два варианта погашения кредита: аннуитетный и дифференцированный платеж.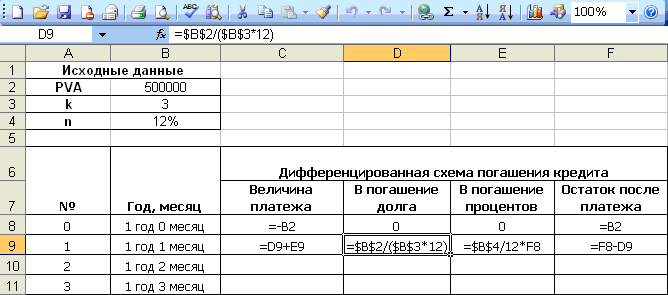
Кредитный рынок предлагает в основном банковские продукты с аннуитетными выплатами. Банки предлагают дифференцированную схему начисления процентов только по долгосрочным кредитам.
Особенности дифференцированных платежей
Дифференцированная схема платежей отличается тем, что к концу периода кредитования сумма платежей по кредиту уменьшается, то есть основная нагрузка заемщика ложится на первоначальный период кредитования.При такой схеме каждый платеж состоит из двух частей. Первая часть — это основной платеж или фиксированная часть, для расчета которой общая сумма кредита делится на равные части. Вторая часть — это переменная, то есть сумма процентов, при этом проценты рассчитываются на остаток долга.
Российские банки редко предлагают кредитные продукты с дифференцированной оплатой. Ведь при такой схеме банки вынуждены предъявлять повышенные требования к платежеспособности своего клиента, поскольку способность клиента погасить ссуду оценивается из расчета первых увеличенных платежей.
Дифференциальные выплаты выгодно использовать только при расчете долгосрочных кредитных продуктов.
Дифференциальные выплаты выгодно использовать только при расчете долгосрочных кредитных продуктов.
Пример расчета дифференциального платежа
Итак, дифференцированный платеж состоит из двух составляющих.
Базовый платеж рассчитывается по следующей формуле:
m = K / N, где
M — основной платеж, K — сумма кредита, N — срок кредита.
Проценты начисляются на остаток долга, который рассчитывается по формуле:
Kn = K — (m * n), где
n — количество уже прошедших периодов.
Тогда переменная часть — сумма процентов будет рассчитана следующим образом:
p = Kn * P / 12, где
p — сумма начисленных процентов за период, P — годовая процентная ставка, Kn — остаток. долга на начало каждого периода.
Ставка по кредиту делится на 12, т.к. расчет ежемесячных платежей.
Самый простой способ понять, что такое дифференцированные платежи, на примере расчета.
Составьте график платежей по кредиту в размере 150000 рублей, годовая процентная ставка по кредиту составляет 14%, а срок кредита — 6 месяцев. Постоянная часть платежа будет:
150000/6 = 25000.
Тогда график дифференцированных платежей будет следующим:
Первый платеж: 25000 + 150000 * 0,14 / 12 = 26750
Второй платеж: 25000 + (150000 — (25000 * 1)) * 0.14/12 = 26458,33
Третий платеж: 25000 + (150000 — (25000 * 2)) * 0,14 / 12 = 26166,66
Четвертый платеж: 25000 + (150000 — (25000 * 3)) * 0,14 / 12 = 25875
пятый платеж: 25000 + (150000 — (25000 * 4)) * 0,14 / 12 = 25583,33
Шестой месяц: 25000 + (150000 — (25000 * 5)) * 0,14 / 12 = 25291,67
Тогда общая сумма процентных выплат по кредиту будет:
26750 + 26458.33 + 26166.66 + 25875 + 25583.33 + 25291.67 — 150000 = 6124.99
- Аннуитетные или дифференцированные выплаты: что для заемщика более выгодно в 2019 году
6.{2} -5x + 6} {x-2} \\ & = \ гидроразрыва {(x-3) (x-2)} {x-2} \\ & = х-3 \\ f ‘(x) & = \ текст {1} \ end {align *}
Найдите \ ({f} ‘\ left (y \ right) \), если \ (f \ left (y \ right) = \ sqrt {y} \).
{3} +2 \ sqrt {x} -3} {x} \).{2}}
\ end {выровнять *}
Найдите \ (\ frac {dy} {dx} \), если \ (x = 2y + 3 \).
Сделайте \ (y \) предметом формулы, чтобы различать \ (y \) относительно \ (x \).
\ begin {align *} y & = \ frac {1} {2} x — \ frac {3} {2} \\ \ поэтому \ frac {dy} {dx} & = \ frac {1} {2} \ end {выровнять *} Определить \ (f ‘(\ theta) \), если \ (f (\ theta) = 2 (\ theta ^ {\ frac {3} {2}} —
3 \ theta ^ {- \ frac {1} {2}}) ^ {2} \).
{\ frac {3} {2}}}
\ end {выровнять *}
Текущая стоимость Vs. Будущая стоимость аннуитетов
Приведенная стоимость и будущая стоимость — это термины, которые часто используются в аннуитетных договорах. Текущая стоимость аннуитета — это сумма, которую необходимо инвестировать сейчас, чтобы гарантировать желаемый платеж в будущем, а ее будущая стоимость — это общая сумма, которая будет достигнута с течением времени.
Что такое аннуитет?
Аннуитет — это финансовое вложение, обеспечивающее регулярные выплаты в течение определенного периода времени.В наше время аннуитет чаще всего приобретается через страховую компанию или компанию, предоставляющую финансовые услуги.
Ключевые выводы
- Приведенная стоимость — это сумма денег, которую необходимо инвестировать для достижения конкретной будущей цели.
- Будущая стоимость — это сумма в долларах, которая будет накапливаться со временем, когда эта сумма будет инвестирована.
- Текущая стоимость — это сумма, которую вы должны инвестировать, чтобы реализовать будущую стоимость.
Этот тип инвестиций часто используется теми, кто готовится к выходу на пенсию или в период плановой безработицы.В зависимости от выбора инвестора аннуитет может приносить фиксированный или переменный доход.
Когда вы покупаете аннуитет, страховая компания берет сразу единовременную сумму денег и инвестирует ее за вычетом взимаемых комиссий. В свою очередь, инвестор будет получать оговоренную сумму денег через равные промежутки времени в течение определенного периода времени.
Различные опции
Есть множество вариантов аранжировки. Выплаты могут начаться немедленно или могут быть отложены на дату в будущем, когда инвестор будет готов уйти на пенсию.
Некоторые платят до смерти бенефициара, тем самым перекладывая риск долголетия с бенефициара на страховую компанию. Пары часто принимают меры, чтобы выплаты продолжались на протяжении всей жизни выжившего партнера.
Текущая стоимость и будущая стоимость зависят от многих индивидуальных переменных.
Все эти решения влияют на точную сумму, которую получатель получит в виде ежемесячного ежегодного платежа.
Расчет как настоящей, так и будущей стоимости предполагает регулярную ренту с фиксированной скоростью роста.Многие онлайн-калькуляторы определяют как настоящую, так и будущую стоимость аннуитета, учитывая его процентную ставку, сумму платежа и продолжительность.
Текущая стоимость аннуитета
Приведенная стоимость аннуитета — это текущая стоимость всего дохода, который будет получен от этих инвестиций в будущем. С практической точки зрения, это сумма денег, которую нужно будет инвестировать сегодня, чтобы получить определенный доход в будущем.
Используя процентную ставку, желаемую сумму платежа и количество платежей, расчет приведенной стоимости дисконтирует стоимость будущих платежей для определения вклада, необходимого для получения и поддержания фиксированных платежей в течение установленного периода времени.
Например, формула приведенной стоимости может использоваться для определения того, сколько инвестировать сейчас, если вы хотите гарантировать ежемесячные платежи в размере 1000 долларов в течение 10 лет. Чтобы получить ежегодный платеж в размере 1000 долларов США на 10 лет с процентной ставкой 8%, вам нужно будет инвестировать 6 710,08 долларов США сегодня.
Будущая стоимость ренты
Будущая стоимость аннуитета представляет собой общую сумму денег, которая будет начислена за счет последовательных инвестиций в течение установленного периода со сложными процентами.
Вместо того, чтобы планировать гарантированную сумму дохода в будущем, вычисляя, сколько нужно инвестировать сейчас, эта формула оценивает рост сбережений при фиксированной ставке инвестиций в течение заданного периода времени.
Расчет будущей стоимости будет использоваться для оценки баланса инвестиционного счета, включая рост процентов, после внесения ежемесячных взносов в размере 1000 долларов США в течение 10 лет.
В этом случае предположим, что процентная ставка составляет 8% (что также является темпом роста), через 10 лет будущая стоимость составит 19 990 долларов.05.
Дифференциальные уравнения — Введение
Дифференциальное уравнение — это уравнение с функцией и одной или несколькими производными:
Пример: уравнение с функцией y и ее производная dy dx
Решение
Мы решаем , когда обнаруживаем функцию y (или набор функций y).
Есть много «уловок» для решения дифференциальных уравнений (, если их можно решить!).
Но сначала: почему?
Почему полезны дифференциальные уравнения?
В нашем мире вещи меняются, и , описывающий, как они меняются, часто заканчивается дифференциальным уравнением:
Пример: кролики!
Чем больше у нас кроликов, тем больше у нас кроликов.
Тогда эти кролики вырастут и тоже родят детей! Население будет расти все быстрее и быстрее.
Важными частями этого являются:
- Население N в любое время т
- темп роста р
- Скорость изменения населения dN dt
Подумайте о dN dt как о «насколько изменяется население с изменением времени в любой момент времени».
Представим, что скорость роста r составляет 0,01 новых кроликов в неделю на каждого текущего кролика.
Когда популяция составляет 1000 , скорость изменения dN dt составляет 1000 × 0,01 = 10 новых кроликов в неделю.
Но это верно только в конкретное время и не включает тот факт, что население постоянно увеличивается. Чем больше популяция, тем больше у нас кроликов!
Когда население составляет 2000 , мы получаем 2000 × 0.01 = 20 новых кроликов в неделю и т.
Д.
Так что лучше сказать, что скорость изменения (в любой момент) — это скорость роста, умноженная на численность населения в этот момент:
dN dt = rN
И это дифференциальное уравнение , потому что оно имеет функцию N (t) и ее производную.
А какая мощная математика! Это короткое уравнение гласит, что «скорость изменения численности населения с течением времени равна темпам роста, умноженным на численность населения».
Дифференциальные уравнения могут описывать, как меняется население, как движется тепло, как вибрируют пружины, как распадается радиоактивный материал и многое другое. Это очень естественный способ описания многих вещей во Вселенной.
Что с ними делать?
Само по себе дифференциальное уравнение — прекрасный способ выразить что-либо, но его сложно использовать.
Итак, мы пытаемся решить их, превратив дифференциальное уравнение в более простое уравнение без дифференциальных битов, чтобы мы могли выполнять вычисления, строить графики, предсказывать будущее и так далее.
Пример: Сложные проценты
Деньги приносят проценты. Проценты могут рассчитываться в фиксированное время, например, ежегодно, ежемесячно и т. Д., И добавляться к первоначальной сумме.
Это называется сложным процентом.
Но когда он начисляется непрерывно , тогда в любое время проценты добавляются пропорционально текущей стоимости ссуды (или инвестиций).
И по мере роста ссуды проценты по ней увеличиваются.
Используя t для времени, r для процентной ставки и V для текущей стоимости ссуды:
dV dt = rV
И вот что интересно: это то же самое уравнение, которое мы получили с кроликами! Просто у него разные буквы.Итак, математика показывает нам, что эти две вещи ведут себя одинаково.
Решение
Дифференциальное уравнение говорит об этом хорошо, но его трудно использовать.
Но не волнуйтесь, это можно решить (с помощью специального метода, называемого разделением переменных), и в результате получится:
V = Pe rt
Где P — принципал (первоначальный заем), а e — число Эйлера.
Таким образом, непрерывно начисляемый заем в размере 1000 долларов США на 2 года с процентной ставкой 10% становится:
V = 1000 × e (2 × 0.1)
В = 1000 × 1,2 2140 …
V = 1221,40 $ (с точностью до цента)
Итак, дифференциальные уравнения хороши для описания вещей, но их нужно решать, чтобы они были полезными.
Дополнительные примеры дифференциальных уравнений
Уравнение Ферхюльста
Пример: снова кролики!
Помните наше дифференциальное уравнение роста:
dN dt = rN
Что ж, этот рост не может продолжаться вечно, так как у них скоро закончится доступная еда.
Итак, давайте улучшим его, включив:
- максимальное население, которое может содержать еда тыс.
Парень по имени Ферхюльст во всем разобрался и получил это дифференциальное уравнение:
dN dt = rN (1-N / k)
Уравнение Ферхюльста
Простое гармоническое движение
В физике простое гармоническое движение — это тип периодического движения, в котором восстанавливающая сила прямо пропорциональна смещению.
Примером этого является груз на пружине.
Пример: пружина и груз
К пружине прикреплен груз:
- вес опускается под действием силы тяжести,
- при растяжении пружины ее натяжение увеличивается,
- вес замедляется,
- , затем натяжение пружины возвращает ее вверх,
- затем он снова и снова падает, вверх и вниз.
Опишите это математически!
Гиря тянется вниз под действием силы тяжести, и мы знаем из Второго закона Ньютона, что сила равна массе, умноженной на ускорение:
F = m a
А ускорение — это вторая производная положения по времени, поэтому:
F = m d 2 x dt 2
Пружина подтягивает ее вверх в зависимости от того, насколько она растянута ( k — жесткость пружины, а x — степень ее растяжения): F = -kx
Две силы всегда равны:
м d 2 x dt 2 = −kx
У нас есть дифференциальное уравнение!
Имеет функцию x (t) и вторую производную d 2 x дт 2
Примечание: мы не включили «демпфирование» (замедление отскоков из-за трения), которое немного сложнее, но вы можете поиграть с ним здесь (нажмите play ):
Создание дифференциального уравнения является первым важным шагом.
Но нам также нужно решить , чтобы узнать, как, например, пружина со временем подпрыгивает вверх и вниз.
Классифицируйте, прежде чем пытаться решить
Так как же нам решить их?
Это не всегда просто!
За прошедшие годы мудрые люди разработали специальных методов для решения некоторых типов дифференциальных уравнений.
Итак, нам нужно знать , что это за тип дифференциального уравнения.
Это как путешествие: разные виды транспорта решили, как добраться до определенных мест. Это рядом, так что мы можем просто гулять? Есть дорога, по которой мы можем взять машину? Или это в другой галактике, и мы просто еще не можем туда добраться?
Итак, давайте сначала классифицируем дифференциальное уравнение .
Обычное или частичное
Первая основная группа:
- «Обычные дифференциальные уравнения» (ODE) содержат единственную независимую переменную (например, y )
- «Уравнения с частными производными» (PDE) имеют две или более независимых переменных.
Здесь мы изучаем обыкновенных дифференциальных уравнений !
Порядок и степень
Далее прорабатываем Порядок и Степень:
Заказать
Ордер старшая производная (первая производная? Вторая производная и т. Д.):
Пример:
dy dx + y 2 = 5x
Имеет только первую производную dy dx , как и «Первый Орден»
Пример:
d 2 y dx 2 + xy = sin (x)
Имеет вторую производную d 2 y dx 2 , как и «Заказ 2»
Пример:
d 3 y dx 3 + x dy dx + y = e x
Имеет третью производную d 3 y dx 3 который превосходит dy dx , как и «Заказ 3»
градусов
Степень — это показатель высшей производной.
Пример:
( dy dx ) 2 + y = 5x 2
Старшая производная — это просто dy / dx, а ее показатель степени равен 2, так что это «Вторая степень»
На самом деле это обыкновенное дифференциальное уравнение второй степени первого порядка
Пример:
d 3 y dx 3 + ( dy dx ) 2 + y = 5x 2
Старшая производная — это d 3 y / dx 3 , но у нее нет показателя степени (ну, на самом деле показатель степени 1, который не показан), так что это «Первая степень».
(Показатель степени 2 на dy / dx не учитывается, так как это не самая высокая производная).
Итак, это обыкновенное дифференциальное уравнение первой степени третьего порядка
Будьте осторожны, не путайте порядок со степенью. Некоторые люди используют порядок слов, когда имеют в виду степень!
линейный
Это Линейное значение , когда переменная (и ее производные) не имеют показателя степени или другой функции.
Итак, нет y 2 , y 3 , √y, sin (y), ln (y) и т. Д.,
просто y (или любая другая переменная)
Более формально линейное дифференциальное уравнение имеет форму:
dy dx + P (x) y = Q (x)
Решение
Хорошо, мы классифицировали наше дифференциальное уравнение, следующий шаг — решение.
И у нас есть Руководство по решению дифференциальных уравнений, которое поможет вам.
Дифференциальная стоимость — узнайте, как рассчитать дифференциальную стоимость
Что такое дифференциальная стоимость?
Дифференциальная стоимость — это разница между стоимостью двух альтернативных решений. Затраты возникают, когда бизнес сталкивается с несколькими похожими вариантами, и выбор необходимо делать, выбирая один вариант и отбрасывая другой. Когда руководители предприятий сталкиваются с такими ситуациями, они должны выбрать наиболее жизнеспособный вариант, сравнивая затраты и прибыль каждого варианта.
Компании используют дифференциальный анализ затрат для принятия важных решений по долгосрочным и краткосрочным проектам. Дифференциальная стоимость также предоставляет менеджерам количественный анализ, который формирует основу для разработки стратегии компании.
Пример дифференциальной стоимости
Компания ABC — оператор связи, который в основном полагается на объявления в газетах и веб-сайт компании для маркетинга. Однако недавно нанятый директор по маркетингу предлагает компании сосредоточиться на телевизионной рекламе и маркетинге в социальных сетях, чтобы охватить более широкую клиентскую базу.
В настоящее время оператор связи ежемесячно тратит 400 долларов на рекламу в газетах и 100 долларов на поддержку веб-сайта компании. По оценкам директора по маркетингу, он будет тратить на телевизионную рекламу примерно 1000 долларов в месяц. Компании также необходимо будет нанять миллениала за 250 долларов в неделю для наблюдения за ее маркетингом в социальных сетях. Если оператор связи перейдет на новую рекламную технику, он будет тратить 2000 долларов в месяц на рекламные расходы. В этом случае дифференциальная стоимость составляет 1500 долларов (2000–500 долларов).
Компания ABC должна решить, продолжать ли использовать свои текущие рекламные платформы или тратить дополнительные суммы на новые рекламные каналы. Они должны оценить, оправдывают ли потенциальные дополнительные выгоды дополнительных затрат. Получит ли он доступ к более широкой аудитории и увеличит возможность привлечения новых клиентов? Есть ли дополнительные расходы в рамках бюджета? Улучшит ли маркетинг в социальных сетях взаимодействие с существующими клиентами и увеличит продажи?
Учет дифференциальных затрат
Дифференциальные затраты могут представлять собой фиксированные затраты, переменные затраты или их комбинацию.Руководители компании используют дифференциальный анализ затрат, чтобы выбрать один из вариантов для принятия жизнеспособных решений, которые положительно повлияют на компанию. Метод дифференциальной стоимости — это процесс управленческого учета, который ведется в электронных таблицах и не требует бухгалтерских проводок.
Альтернативная стоимость
Альтернативная стоимость Альтернативная стоимость Альтернативная стоимость является одним из ключевых понятий в изучении экономики и преобладает в различных процессах принятия решений. Относится к потенциальным выгодам или доходам, от которых можно отказаться, если предпочитать один вариант другому.Руководители компании должны выбирать между вариантами, но решение следует принимать после рассмотрения альтернативных издержек невыполнения преимуществ, предлагаемых невыбранным вариантом.
В случае ABC Company переход на телевизионную рекламу и маркетинг в социальных сетях открывает перед компанией более широкую клиентскую базу. Если компания заработала 10 000 долларов на текущих маркетинговых платформах, переход на более продвинутые рекламные платформы может привести к увеличению дохода на 40% до 14 000 долларов.
Этот шаг ставит альтернативные издержки использования старого метода рекламы в 4 000 долларов (14 000 — 10 000 долларов).4000 долларов — это доход, который компания ABC отказалась бы от использования старых маркетинговых методов и неспособности принять более сложные маркетинговые модели.
Невосполнимые затраты
Невосполнимые затратыНекоторые затраты Невосполненные затраты — это затраты, которые уже произошли и не могут быть возмещены никаким способом. Невосполненные затраты не зависят от каких-либо событий и не должны относиться к затратам, которые компания уже понесла, но которые не могут быть устранены никаким управленческим решением. Примером может служить ситуация, когда компания покупает машину, которая устаревает в течение короткого периода времени, и продукты, произведенные на этой машине, больше не могут быть проданы клиентам.
Рассмотрим компанию, занимающуюся производством пластиковых пакетов, которая приобретает современное оборудование для удвоения текущего производства пластиковых пакетов. Как только компания вводит новую машину в эксплуатацию, правительство запрещает производство пластиковых пакетов в стране и объявляет преступлением производство или продажу пластиковых пакетов для любого человека. Новое постановление делает машину и производимые пластиковые пакеты устаревшими, и компания не может изменить решение правительства. Это расходы, которые нельзя возместить, или которые являются невозвратными затратами.
Применение дифференциальной стоимости
Менеджеры используют дифференциальные затраты следующим образом:
1. Определение наиболее прибыльного уровня производства и цены
Когда компания хочет определить идеальный уровень производства, который дает самый высокий доход или самая высокая чистая прибыль, он должен провести исследование рынка, чтобы определить отпускные цены на свою продукцию на различных уровнях деятельности. Затем компания рассчитывает предполагаемую выручку, умножая ожидаемый объем производства на определенном уровне на отпускную цену.
Дифференциальный доход получается путем вычитания продаж на одном уровне деятельности из продаж предыдущего уровня. Дифференциальная стоимость сравнивается с дифференциальной выручкой, чтобы определить наиболее прибыльный уровень производства и лучшую отпускную цену. Руководство примет решение об увеличении уровня производства, когда дифференциальная выручка превышает дифференциальную стоимость.
2. Предложите коммерческое предложение по более низкой цене продажи для увеличения производственных мощностей
Когда компания хочет расширить свои производственные мощности, руководство может снизить продажную цену для увеличения продаж.Компания снижает отпускную цену до уровня, при котором компания по-прежнему будет получать прибыль и покрывать производственные затраты.
Чтобы компания знала, жизнеспособна ли новая цена продажи, она рассчитывает дифференциальную стоимость, вычитая стоимость текущей мощности из стоимости предлагаемой новой мощности. Затем дифференциальная стоимость делится на увеличенное количество единиц продукции, чтобы определить минимальную продажную цену. Любая цена, превышающая эту минимальную продажную цену, представляет собой дополнительную прибыль для компании.
Другие ресурсы
CFI — официальный глобальный провайдер аналитики финансового моделирования и оценки (FMVA) ® Стать сертифицированным аналитиком финансового моделирования и оценки (FMVA) ® Сертификация CFI по финансовому моделированию и оценке (FMVA) ® поможет вы обретете необходимую уверенность в своей финансовой карьере. Запишитесь сегодня! звание ведущей программы сертификации финансовых аналитиков. Чтобы продолжить обучение и продвигаться по карьерной лестнице, вам будут полезны следующие дополнительные ресурсы CFI:
- Анализ поведения затрат Анализ поведения затрат Анализ поведения затрат означает попытку руководства понять, как изменяются операционные затраты в связи с изменением структуры затрат
- Структура затрат Структура затрат относится к типам расходов, которые несет бизнес, и обычно состоит из постоянных и переменных затрат.Постоянные затраты остаются неизменными
- Формула предельных затрат Формула предельных затрат Формула предельных затрат представляет дополнительные затраты, понесенные при производстве дополнительных единиц товара или услуги. Предельные затраты
- Прогнозирование статей отчета о прибылях и убытках Прогнозирование статей отчета о прибылях и убытках Мы обсуждаем различные методы прогнозирования статей отчета о прибылях и убытках. Прогнозирование отдельных статей отчета о прибылях и убытках начинается с выручки от продаж, затем начинается стоимость
Как рассчитать приведенную стоимость будущих арендных платежей
FV / (1 + r) n
Где
- FV — будущая стоимость
- r — требуемая норма прибыли
- n — количество периодов
Когда вы используете функцию PV в Excel, она подробно описывает аргументы, используемые в функции
Ставка: Процент ставка за период.Например, если вы получаете автомобильную ссуду под 10 процентов годовых и делаете ежемесячные платежи, ваша процентная ставка в месяц составляет 10% / 12, или 0,83%. Вы должны ввести 10% / 12, или 0,83%, или 0,0083, в формулу в качестве ставки.
Кол-во: Общее количество периодов выплат в аннуитете. Например, если вы получаете четырехлетний автокредит и делаете ежемесячные платежи, ваш кредит будет иметь 4 * 12 (или 48) периодов. Вы должны ввести 48 в формулу для кпер.
Pmt: Выплата производится каждый период и не может измениться в течение срока действия аннуитета.Обычно PMT включает основную сумму и проценты, но не другие сборы или налоги. Например, ежемесячные платежи по ссуде на покупку автомобиля на четыре года под 12 процентов в размере 10 000 долларов составляют 263,33 доллара США. Вы должны ввести -263,33 в формулу как pmt. Если pmt не указан, необходимо указать аргумент fv.
FV: Будущая стоимость или остаток денежных средств, который вы хотите получить после совершения последнего платежа. Если fv опущено, предполагается, что оно равно 0 (например, будущая стоимость ссуды равна 0). Например, если вы хотите сэкономить 50 000 долларов на оплату специального проекта через 18 лет, тогда 50 000 долларов — это будущая стоимость.Затем вы можете сделать консервативное предположение о процентной ставке и определить, сколько вы должны откладывать каждый месяц. Если fv опущено, вы должны включить аргумент pmt.
Тип: Число 0 или 1 указывает срок выплаты.
Как рассчитывается это число?
Как показано на скриншоте, вам необходимо:
- Добавить будущие денежные потоки, причитающиеся арендодателю
- Добавить период, к которому в данном случае относятся денежные потоки от 0 до 9
- Определить ставку дисконтирования чтобы представить стоимость будущих платежей в этом примере 6%
Каждый отдельный период оценивается по текущей стоимости, и общая сумма этих цифр равна 9 585 долларам.98.
Ключевым моментом в этой функции Excel по приведенной стоимости является присвоение каждому платежу периода. Первый период равен 0, что приводит к сумме приведенной стоимости в 1000 долларов США, если это не будущая сумма. С другой стороны, в периоде 1 приведенная стоимость 1 050 составляет 990,57 долларов.
Это показывает, насколько важен период или «Nper» в Excel, учитывая, что это ввод периода, а не ввод даты.
Система дифференциальной пошлины Тейлора (формула и расчет)
Система дифференциальной сдельной ставки Тейлора (формула и расчет)!
Система дифференциальной сдельной оплатыбыла введена Тейлором, отцом научного менеджмента.Основополагающий принцип этой системы состоит в том, чтобы наказать медленного рабочего, выплачивая ему низкую сдельную ставку за низкую производительность, и вознаградить эффективного рабочего, дав ему более высокую сдельную плату за более высокую производительность. Тейлор придерживался мнения, что неэффективному работнику не должно быть места в организации, и он должен быть вынужден покинуть организацию, выплачивая ему низкую сдельную оплату за низкую производительность.
Тейлор исходил из предположения, что с помощью изучения времени и движения можно установить стандартное время для выполнения конкретной задачи.Чтобы побудить рабочих завершить работу в течение стандартного времени, Тейлор выступал за две сдельные ставки, так что, если рабочий выполняет работу в пределах или меньше стандартного времени, он должен увеличивать сдельную оплату, а если он не выполняет сдельную оплату. работая в установленное время, ему предоставляется меньшая сдельная ставка.
Таким образом, если стандартное производство было установлено на уровне 8 единиц в день по 8 часов (принимая нормальную сдельную ставку как Re 1), более высокая сдельная ставка для 8 единиц или более может составлять 1,20 рупий за единицу, а более низкая ставка — для продукции. менее 8 единиц в сутки, может быть 80 П.на единицу.
Следовательно, Тейлор решил дать крупное вознаграждение тем, кто завершит работу в пределах или меньше стандартного времени, и гораздо меньшую заработную плату тем, кто не завершит работу в установленные сроки. Система очень жестока по отношению к неэффективным работникам, потому что они получают гораздо меньшую заработную плату из-за более низкой производительности и более низких ставок.
Более того, этот метод не гарантирует минимальную заработную плату. Другой недостаток системы заключается в том, что если рабочий просто не выполняет работу в течение стандартного времени, он получает гораздо меньшую заработную плату, чем рабочий, который просто завершает работу в течение стандартного времени.Таким образом, сейчас система практически не используется.
Иллюстрация:
Рассчитайте заработок рабочих A и B по прямой сдельной системе и дифференциальной сдельной системе Тейлора, используя следующие данные:
Обычная ставка в час = 1,80 рупий
Стандартное время на единицу = 20 секунд
Применяемые дифференциалы:
80% сдельной ставки ниже нормы
120% сдельной ставки по норме и выше.
Рабочий A производит 1300 единиц в день, а рабочий B производит 1500 единиц в день.